As I mentioned, my checkers-playing AI is on hold until I have a few more viable tools available to do what’s necessary. However, since no matter what I do, I can’t stop thinking about the problem, it occurs to me that there is some work to be done in which I believe I can at least make some progress. Because regardless of how I ultimately design the NN that does the learning, I’m going to need to represent the input (the state) and the output (the action). Right now, I don’t really have a good sense for how I’m going to represent either.

For tic tac toe, while there were some details that I was going to have to optimize, it’s a fairly simple problem. The input is the discrete board states. With nine positions and three possible states for each position (X, O, and blank), one straightforward way to set it up would be with 27 inputs (9 positions and three states for each input). Since, in tic tac toe, there are, at max, 9 possible next moves, the output is simple: 9 nodes. Which means that regardless of the NN in the middle, we’d have something like this:

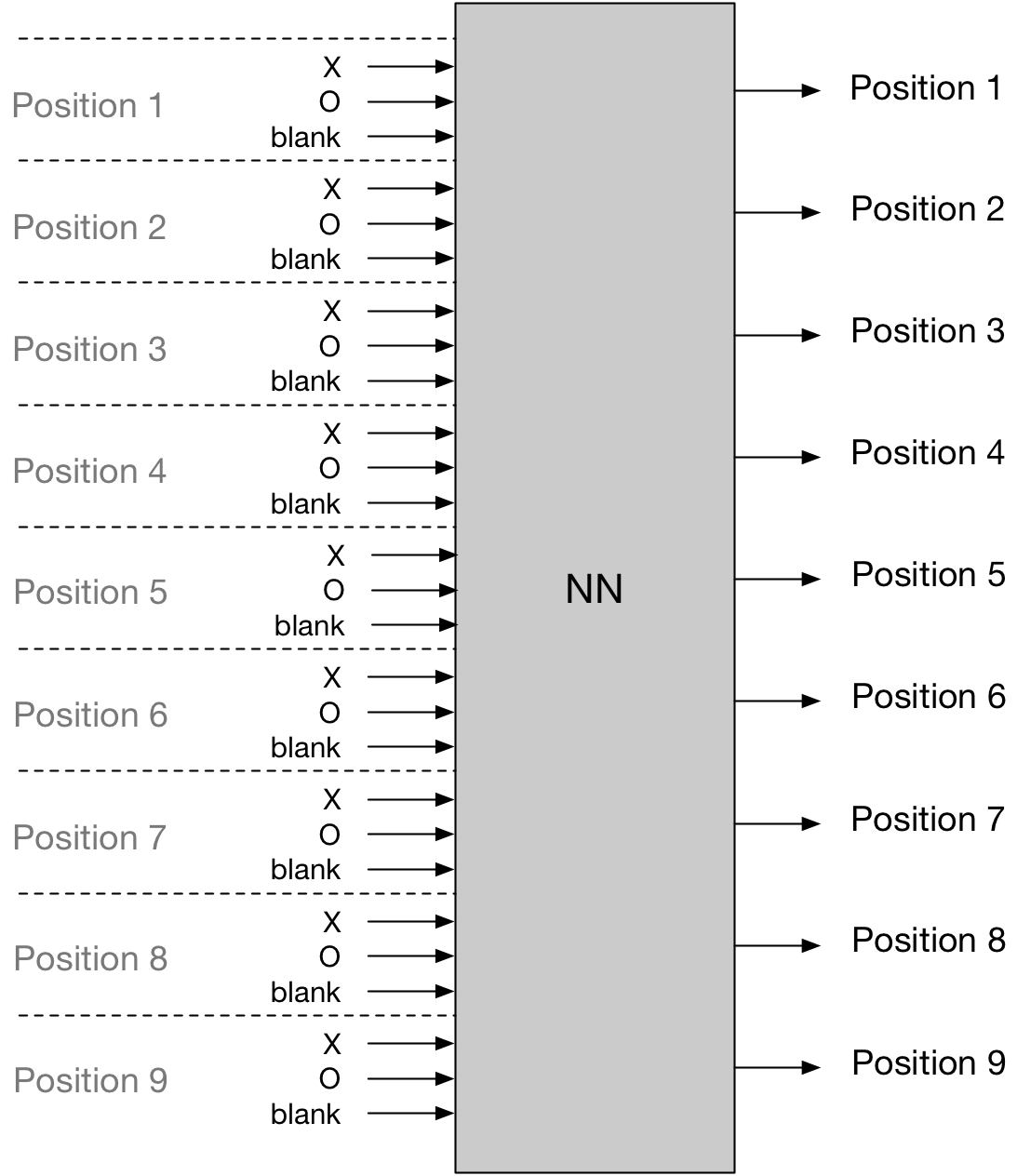
Here are the only two details I wasn’t sure about. First, it seems possible that for the inputs you could have just 9 inputs with different input values for O, X, and blank. It was really just down to which would do better performance wise in a NN. The other, more involved question was how to handle the rules of the game. That is, illegal moves. I had more or less decided that I would just train the system to not make them, but it still seems possible that one could essentially “hard code” what moves are legal and illegal. I still don’t have a sense for how one would hard code that, and furthermore, it seems more in the spirit of the exercise to have the system learn on its own to make only legal moves.

Checkers, however, is more complicated. The input side of things, at least at first glance, seems straightforward but with some twists. Here’s the board:

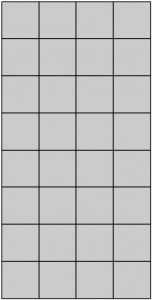
There are 64 squares, but only the dark squares are board positions, so if we compress horizontally (which makes more visual sense to see what moves are legal) we get an 8×4 board of 32 squares.

Given that only diagonal moves are legal, we can see how that maps to this compressed board by showing paths for legal, non-jump moves.

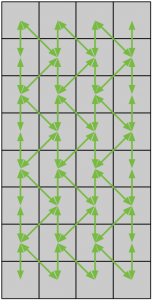
So there are nuances to the game board state, but nothing that couldn’t be easily accommodated. The issue, though pertains to the actions for a given board state. It’s more complicated than tic tac toe where the universe of possible moves is simply the 9 board positions, with some being legal (vacant positions) and some being illegal (occupied positions). In checkers, instead placing a piece, actions consist of moving one of 12 possible pieces. Thus the domain of possible actions is less directly tied to available board positions than to the pieces themselves.

There are two further complications as well. First is the fact that there is the possibility that there can be multiple jumps available to a given piece which means the possibility of multiple moves on a given turn. Second, there is the issue of crowning a piece which gives the piece the newfound ability to move both forward and backward on the board.

Epiphany

As I’ve been talking this out on paper (so to speak), things started to come together and I had a small epiphany. With tic tac toe, and my experience with fully-connected NNs, I had been thinking about the board as a whole. That is, taking into account the entire board, what would be the best place to drop the X. With a maximum of only 9 possible locations, this made sense.

My thought about the domain of possible actions being tied to individual pieces rather than board positions led me to consider the fact that any AI model will, at some point, have to evaluate the options available to an individual piece independent of other possibilities. So while ultimately any analysis the system does will have to be carried out for all pieces, it would necessarily start by analyzing the possibilities available to an individual piece. And it seems possible that a single NN, with the proper architecture and inputs, could be applied sequentially to each piece on the board. The analysis of each piece would produce some preference as to which was the best move. That preference would need to then be compared to the preference for the remainder of the pieces. One move by one piece would win (not the game, but the evaluation), and that would be the move that would be chosen.

Since a crowned piece would have a different fundamental domain of possible moves, it would seem to make sense to train and apply a different NN for crowned pieces. So what might this look like?

A regular piece only has, at most, two possible moves available to it. A crowned piece has a maximum of four. thus, one could have two NNs that might look something like this:

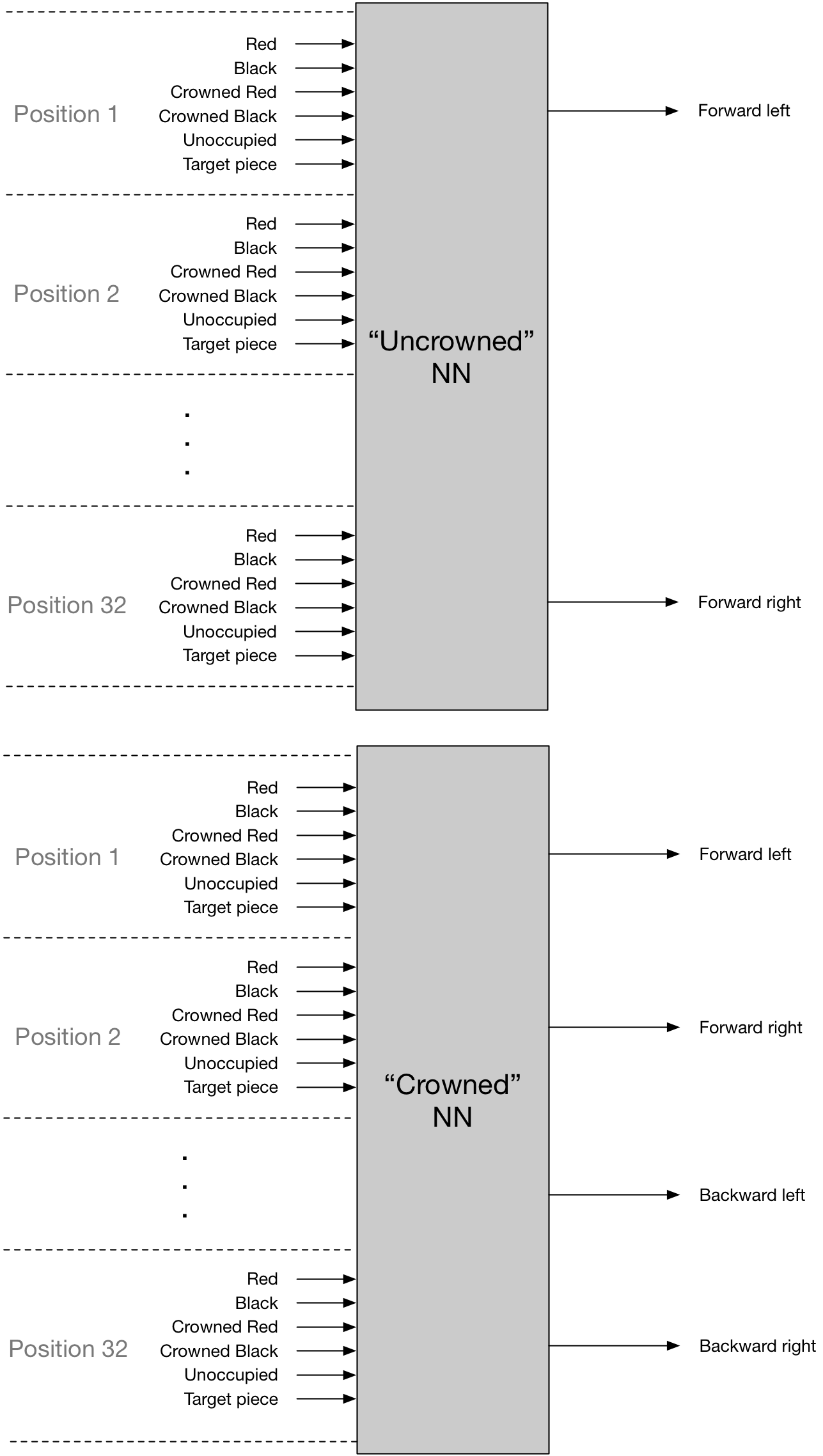
In both NNs, for all squares on the board, the system would take as input whether that square was occupied by a red, crowned red, black, crowned black piece or whether it was unoccupied. It would also capture, for the analysis, whether that square was the “target” piece — that is, the piece being analyzed for the move.  There would be two possible outputs for the uncrowned NN, and four four the crowned NN. This seems build in all the basic input states.

There are however, more output states than are accounted for here. First jumps aren’t explicitly accounted for. This is related to illegal moves. It seems that you could either have four possible output moves (forward left, forward left jump, forward right, forward right jump) or you could just have the two shown, and when there was an opposing piece in the way and an unoccupied space beyond, simply interpret, for instance, a forward left as a forward left jump. Any other forward left scenario (either a same-side piece in that spot or both forward left positions occupied) could be counted as an illegal move. Which brings to mind how to handle illegal moves. By having different crowned and uncrowned NNs, we’re effectively hard coding at least one important rule. Once could do the same with illegal vs. legal moves. But I’m still inclined to want to have the NN learn that for real.

Also, in double-jump scenarios where there is more than one possible second jump, the output state does not capture that. However, it would seem that each network could be used recursively to accommodate that scenario.

And finally, there would need to be some way to handle figuring out which piece/move to choose. On the one hand, it could simply be the move that comes up with the highest value for the output. But upon further thought it would seem that a better way to do that would be to have the outputs themselves hooked up to another NN and have that make the decision. There are significant questions to how this might work. For instance, how to even connect it to the first phase? And more importantly, what is its purpose as differentiated from the first phase, and thus, how would it work?

Either way, though, it occurs to me that I think I may have enough to start building something here. The first phase has elements of a convolutional NN, although it’s not quite the same thing. I could definitely build the repeating crowned an uncrowned NNs as fully connected. And to do this in a way that would be practical to actually use will involve a fair amount of infrastructure which could only be helpful in developing the various supporting skills I’ll need. I think I’ll get going.